introduction
| |
| Visual |
| Electromagnetic |
| Quantum physics |
| Thermodynamics |
| Fluid mechanics (Fluid mechanics is the branch of physics that studies fluid flows…) |
| mechanical (In common parlance, mechanics is the field of machines, engines, vehicles, organs, etc.) |
| Relativity (Special relativity is the formal theory developed by Albert Einstein…) |
| Black hole (In astrophysics, a black hole is a massive object whose gravitational field is extremely strong…) |
| Vector analysis (Vector analysis is a branch of mathematics that studies areas…) |
Ratings
The formulas define the passage between coordinates (R, s ) for an event in the inertial frame PinnedLet’s say it Land (Earth is the third planet in the solar system in terms of distance…)and coordinates (R’, s ) for the same event in the tag MovingLet’s say rocket (Rocket may refer to:)which moves along an axis s with Speed (We distinguish:) Fifth.
It is assumed that the origins time (Time is a concept that humans developed to understand…) Coinciding with the
is put :
Constants of special relativity
there amount (Quantity is a general metrological term (account, amount); numerical,…) Next is fixed in changing coordinates
And determines Clean time (In the theory of relativity, we call the time of a particle the time measured by…)
angle parameter
To simplify the formulas, it is useful to introduce the angular parameter defined by the following formulas:
also
Using this parameter we can write:
Time dilation
If a rocket clock measures duration 

The duration measured by an external standard is always greater than the own duration.
Lorentz transformations
Which gives in matrix form (easier to visualize):
Using hyperbolic functions forcorner (In geometry, the general concept of angle is divided into several concepts…) θwe obtain expressions similar to the formulas for changing the coordinate axes by rotating the plane:
in sense (SENS (Engineered Neglected Aging Strategies) is a scientific project aiming to…) reflects (In mathematics, the inverse of the x element of the set is given by a law…)
or
Law of formation of velocities
A projectile is fired at the missile quickly Th Relative to the reference of this missile, in the direction of movement. Speed Th of shell relative to Earth
Using angle parameters
We have the additional law
Length contraction
If the missile Length (The length of a body is the distance between its two extremes…) to’ In its own standard, its length to It is measured by the distance between two points on the ground that correspond to the front and rear of the missile at the same time Moment (An instant defines the smallest component of time. A moment is not…) (in the ground), so it corresponds to 
The length measured on the ground is smaller than the length of the rocket.
Kinetic energy
to’Kinetic energy (Kinetic energy (also called in ancient writings vis viva, or living force) is…) Of particles it is
to
And for
Quadruple energy driving force
like
we’ve got
At low speeds
We still have the relationship
The following quantity is constant in changing the reference
to Photon (In particle physics, a photon (often symbolized by the letter γ — gamma)…), M = 0 f
Doppler-Fizeau effect

Doppler effect





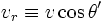
At low speeds
ifa star (A star is a celestial body that emits light independently, such as…) walks away, Fifth is positive, cosθ’ is negative, 
Light diffraction phenomenon:

“Hardcore beer fanatic. Falls down a lot. Professional coffee fan. Music ninja.”






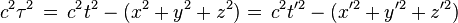


 also
also 




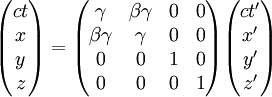





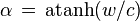

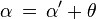
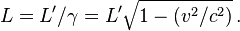
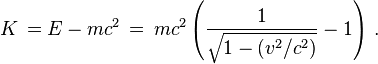

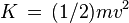

![K \simeq E \simeq pc = \frac{mc^2}{\sqrt{2(1-\beta)}}\equiv \frac{mc^2}{\sqrt{2[1-(v/c)]}}\,.](https://www.techno-science.net/illustration/Definitions/autres/a/acc25fffc50d7155b19484633067d1eb_ae3ee2ea8d8dfdb151e7d0df9fdb0fcd.png)



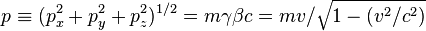




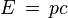


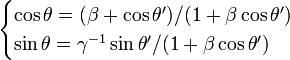
More Stories
Word, Excel, and PowerPoint are free
This magnificent crater bears witness to the existence of water ice on Mars
Discovery of the first rocky atmosphere of an exoplanet on Cancri 55 e