Good point for the James Webb telescope

On December 25, 2021, an Ariane 5 rocket took off from Kourou, Guyana, with a space telescope on board. James Webb (JWST). It reached its destination thirty days later at a distance of about 1.5 million kilometers from Earth, in a direction opposite to that of the Sun. There, it is now orbiting a point in space that orbits the Sun at the same rate as the Earth’s rotation. What’s even more surprising is that at this particular point, we don’t find…nothing! How is this possible? is about nothing? The answer is found in the work of the French mathematician and physicist Joseph-Louis Lagrange. at eighteen^{And the} century, showed that there are five points of this type for the Earth-Sun system. Let’s find out the physical origin of these “Lagrangian points” and their advantages for astronomy and space exploration.

The movement of two massive bodies in the interaction of gravity is particularly simple and elegant. Paths are circles, ellipses, parabolas, hyperbolas, or, in mathematical terms, cones. What about the three bodies? Newton asked the question while thinking about the effect of the Sun on the Moon’s revolution around the Earth, but as mathematician Henri Poincaré well understood two hundred years later, passing two to three masses changes everything: Paths can be varied, incredibly complex and chaotic in nature! Although new results are published regularly, we can consider that this “three-body problem” will not be completely solved in practice.

As any good physicist, it’s urgent to simplify: What happens when one of the three masses is small enough compared to the other two to have little effect on its motion? So we can first determine the trajectory of the two most massive bodies (conical shape), and then study the movement of the third body. While interested in this position, frequent in celestial mechanics, Lagrange discovered his famous points.

Take the state of the sun, earth and a satellite like JWST. The Earth has an almost circular orbit around the center of mass of the Earth-Sun system, and this center, given the ratio of the two masses, located inside the Sun, is slightly offset from the center of the star. Let us now consider a frame of reference whose origin is this center of mass whose axes rotate at the same speed as the Earth, that is, the frame of reference where the Sun and the Earth are stationary. Lagrange showed that there are five given positions in this frame of reference so that if an object were placed there, it would remain motionless. This means that in practice, these objects orbit the center of mass of the Earth-Sun system in a circular path with the same angular velocity as the Earth. At these points, the sum of the two gravitational forces that the body experiences from the Sun and the Earth are completely offset by the centrifugal force that tends to move it away from the center of mass of the Earth and the Sun.

In order to better understand the properties of these points, especially what is happening in their vicinity, a representation of the potential energy of the satellite, the sum of gravitational and centrifugal energies, according to its location is useful. Lagrange points are equilibrium points in this frame of reference, the places where this potential has a maximum, which corresponds to a total power of zero. Unfortunately, none of these extreme values ​​are a “sink” of potential energy, and they are all “pillars” or “peaks”: this means that the equilibrium at these points should not be stable; At the slightest disturbance, the satellite must move away indefinitely.

This is without taking into account the Coriolis force, this force of inertia that depends on the speed and is responsible for the direction of rotation of the trade winds on Earth or the rotation of the Foucault pendulum. Physicists have shown that it establishes equilibrium at points L₄ and me₅ Provided that the mass of the planet is less than 3.8% of the mass of the Sun, this is the case for all those in the Solar System.

Thus, at these points, a prolonged existence of celestial bodies is quite possible. In the case of the Sun-Earth system, an asteroid received a 2010 TK . designation₇ It is located at point L.₄ In 2010, the Latest, 2020 XL₅recently, at point L.₅. Perhaps because of the disturbances caused by other planets? This point is actually 150 million kilometers from Earth, and Jupiter’s gravitational field is greater there. On the contraryAccumulation of asteroids around points L.₄ and me₅ The Sun and Jupiter, the largest planets by mass: They are called “Trojans”, they form somewhat lax clouds along the orbit of Jupiter, and, as seen from this planet, seem to circle the Lagrangian points on very long paths, according to the forecasts of the analysis stability.

very useful points

So what is a file JWST near L.₂ ? It joins the long list of spacecraft already placed in this place (satellites WMAPAnd the HerschelAnd the plank And the Jaya, which is still present), ignoring its instability. Several reasons can be invoked: firstly, these points are not too far from the ground; So, precisely because of this instability, we are certain that no orb is likely to disturb the mission; Finally, the L District.₂ It remains an area where the residual force balance is low, and thus it is much easier to correct or alter the trajectory there by turning on the thrusters than it is to an area with a higher force field. This latter property is also at the heart of the design of the interplanetary transport network, a set of gravitational paths through the solar system that require little energy to traverse, and corrections are made precisely near the associated Lagrangian points. Various pairs of Sun Planet. If energy sobriety is required in such transits, the corresponding travel time is much longer.

Returning to the Lagrange points, for₁ It has the same properties as L.₂ But it is more suitable for observing the sun, as with a satellite SOHO, rather than deep space. Finally, there is a deeper reason to use Lagrange points: since Poincaré, we know that there are indeed families of semi-periodic paths, not necessarily in the plane of the ecliptic and sometimes semi-closed (one speaks of halo orbits) near these points, including the unstable L₁and me₂ . For a satellite in such an orbit, the cost of keeping it there despite the inherent instability of the orbit and other potential perturbations (in the case of JWSTFor example, the sunscreen that protects it under the full force of the pressure of light radiation from our star) is very limited. to me JWSTThis cost is equivalent to increasing its speed by 2.5 meters per second each year. The chosen orbit is located at a good distance from L.₂: away from it from 250,000 to 832,000 km.

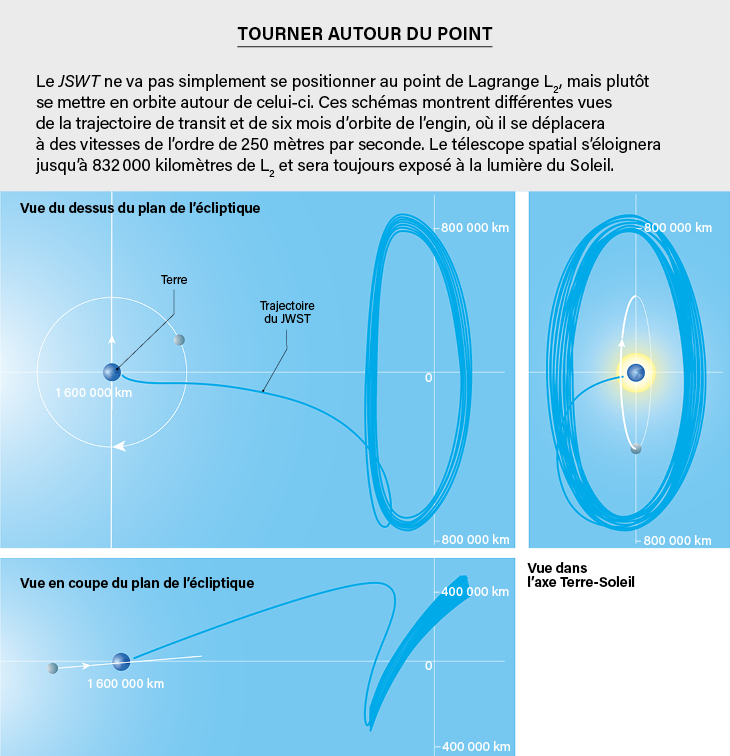
Thanks to its tilt relative to the ecliptic, the telescope will never be in the shadow of the Earth or the Moon: it is enough to maintain constant contact with the Earth and to avoid differences in illumination that can disturb the instrument’s delicate thermal balance. me₂very convenient Jaya and the JWST almost Euclid And the Nancy Grace RomanTwo more space telescopes!